Движенья нет-сказал мудрец брадатый
Другой смолчал и стал пред ним ходить...
Сильнее он не смог бы возразить.
Когда заходит речь о «вечном двигателе», то обычно обсуждению подвергается либо, так называемый, «perpetuum mobile» I-го рода, либо II-го. Такую градацию определила, как я понимаю, история их изобретений. Хотя понятно, что вечного ничего не бывает, все определяет моторесурс механизма, а название это довольно таки условно. Тем не менее, еще на заре цивилизации делались попытки людьми создать такой механизм, который в механической системе позволял бы получать энергию больше затраченной, что и определило название. В те времена создавались только простые механизмы, поэтому и стремились получать ее только чисто механическим способом.
Поможет выбрать и купить диплом, обеспечивая его соответствие всем стандартам качества. Такой документ будет выглядеть официально и надёжно, что даст уверенность при трудоустройстве.
Это и отражало признак «вечного двигателя» 1-го рода. Позже, после открытия законов термодинамики, появилось понятие «вечного двигателя» 2-го рода, который позволял бы получать дополнительную энергию, используя внутреннюю энергию термодинамической системы. О том, чтобы оба признака присутствовали в одном механизме, речи как-то не возникало, видимо считалось, что если невозможно построить по отдельности каждый двигатель, то по совокупности и подавно. Хотя понятие «вечный» уже давно имеет отрицательный оттенок, я все же рискну обосновать затронутую тему, понимая, что шансов у меня никаких, иначе бы мы давно уже пользовались плодами труда этого чуда, а не ухудшали экологию планеты существующими ныне способами добычи энергии. Проблема в том, что работе такого механизма препятствует закон сохранения энергии. Так утверждают ученые, и об этом все знают. Все бы было хорошо, и можно было на этом поставить точку, но дело в том, что закон сохранения энергии оставил «лазейку» для сомнений. Он справедлив только для замкнутых систем. Что такое замкнутая система, состоит ли наш мир из замкнутых систем, как ее определить,- вопрос не совсем простой. Может это и давало повод, вплоть до настоящего времени, любителям, энтузиастам, и всем, кому не лень, изобретать вечный двигатель. К какой категории себя отнести, я не знаю. Можно даже к последней. Тем не менее, я хотел бы донести идею воплощения двух признаков «вечного двигателя» в одном механизме и его реализацию до умов, желающих услышать. Пусть это будет еще одним поводом для улыбок скептиков, по меньшей мере. Для тех же, кто, хотя бы из любопытства, хотел бы узнать, о чем идет речь, изложу свои рассуждения. С процессом, о котором пойдет речь, знаком каждый. Это всплывание пузырьков газа в жидкости. Можно просто любоваться видом пузырьков воздуха, всплывающих в аквариуме, или кипящей жидкости. А можно еще и попытаться определить, какую пользу может принести этот процесс и попробовать воплотить его в жизнь. Если есть желание и некоторые познания физики, то можно попытаться что-то из этого извлечь. Заставить же «работать» всплывающий пузырек газа в жидкости несложно. Для этого достаточно прикрыть его сверху перевернутой чашей. От этого суть физических процессов не изменится, а давящий снизу на чашу газ способен заставить ее всплывать под действием силы Архимеда, т. е. совершать полезную работу. Собранные на бесконечной цепи равномерно друг за другом чаши, одетые на шкивы, к одному из которых, в свою очередь, соединен генератор, вырабатывающий электрическую энергию, дают возможность ее получения и потребления. Достаточно подать сжатый газ под нижнюю чашу, который в данном случае является рабочим телом (топливом), и механизм начнет двигаться в жидкости, являющейся рабочей средой. В частном случае - это окружающие нас воздух и вода, вездесущи и доступны.

Подавая под нижнюю чашу компрессором сжатый воздух, вытесняющий воду из-под чаши, мы заставляем левую часть двигателя всплывать. В верхней части, при опрокидывании чаши, газ вытесняется жидкостью, и они, потеряв выталкивающую силу, двигаются вниз, не препятствуя работе всего механизма. Хотелось бы сразу заверить сомневающихся - он способен вращаться, проверено опытом. Согласно закона Архимеда, газ, вытеснивший жидкость, создает подъемную сил, равную весу вытесненной им жидкости, т. е. один литр воздуха в воде создает подъемную силу 1 кгС =10 Н.Для сравнения, у ртути она более чем в 13 раз выше. Из законов механики известно, что мощность определяется как произведение силы на скорость в точке приложения этой силы. N=FV. Средняя скорость всплытия пузырька с воздухом, а равно и чаши, в воде равна 0.4 м/сек. Отсюда следует, что 1 литр воздуха под чашей движущегося механизма способен развить мощность равную 4 Вт.N=10Н*0,4м/с=4 Вт. У ртути, опять же для сравнения, около 50 Вт. Опираясь на эти расчеты, несложно определить общую мощность любого построенного, так называемого, пневмогидравлического преобразователя энергии. Это все, так сказать, преамбула вопроса. Теперь можно, собственно, и перейти к сути признака «вечного двигателя» 1-го рода. А, поскольку, для его работы нужен сжатый воздух, то и обратимся к техническим характеристикам «среднестатистического» компрессора. К примеру, фирмы «Герц» модели HSC7. Так, по условиям всасывания, компрессор мощностью 5.5кВт способен сжать 0,85м3/мин до 10Атм, т, е, за одну секунду он сожмет 14 литров воздуха до объема 1.4 лит( для изотермического сжатия) и подаст под нижнюю чашу двигателя. Под давлением 10Атм воздух способен продавить столб воды высотой 100 метров. Эта величина является определяющей для построения двигателя, оптимально использующего энергию компрессора, т. е. рабочая левая сторона механизма должна иметь длину плеча равную ста метрам. На этой длине, через каждые 40см, дабы использовать ежесекундную подачу порции воздуха, можно установить 250 чаш объемом 14л каждая, учитывая расширение воздуха при всплытии. Понятно, что и справа должно находиться такое же количество чаш холостого хода, которые не учитываются при расчете. Теперь можно определить мощность, которую способен развить двигатель, работающий на данном компрессоре. Так общий объем воздуха, находящегося в чашах с учетом его расширения при всплытии, можно найти, как среднюю арифметическую сумму крайних значений воздуха в чашах, умноженную на количество чаш рабочего хода. V=14+1,4/2*250=1925л. Зная, что каждый литр воздуха несет 4 Вт энергии, можно найти общую мощность, развиваемую установкой. N=4*1925=7700Вт=7,7кВт.Сравнивая эту энергию с затраченной, можно определить к.п.д. процесса. Видно, что прирост энергии составил 2,2кВт, что дает 1,4 единицы к.п.д. К этим же результатам можно прийти и другим способом расчета. Для этого нужно определить работу, выполненную компрессором за одну секунду и сравнить ее с работой, полученной при всплытии порции воздуха, поданной компрессором за это же время. Нужно заметить, что не все компрессоры по своим техническим характеристикам, позволяют получать свободную энергию. Видимо это зависит от к.п.д. самого компрессора. Тем не менее, факт прироста энергии в этой механической системе имеет место. Так как данная установка ,по сути ,является аккумулятором работающим с одной порцией газа только сжимая эту порцию с каждым разом чуть сильней и на какой то момент времени, накопит энергии достаточной для преобладания последней над потребленной, что подпадает, как мне кажется, под признак «вечного двигателя»1-го рода. С другой стороны, если обратиться, собственно к теории сжатия газов и, как следствие, к техническим характеристикам существующих компрессоров, то можно обнаружить следующую закономерность. В справочнике З.З. Рахмилевича издательства «Химия» 1989г. «Компрессорные установки» на стр. 96-98 даны графики удельного расхода эл. энергии на сжатие газа для разных типов компрессоров, из которых видно, что работа по сжатию газа меньше, чем получаемая с помощью силы Архимеда.
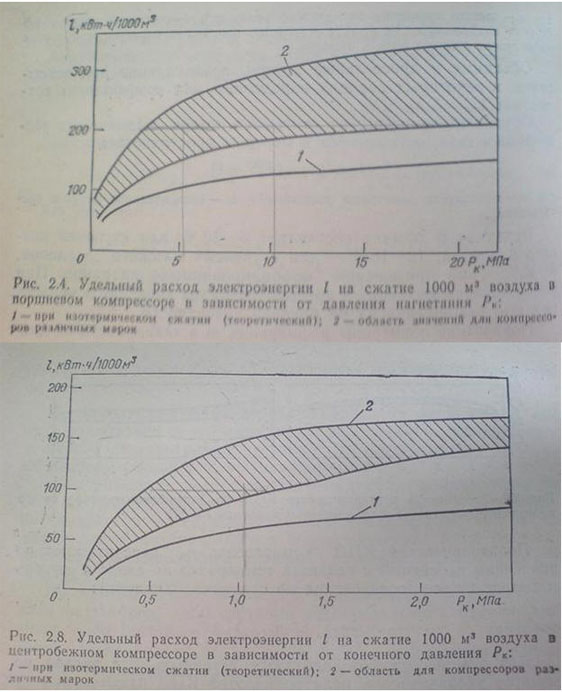
И чем выше давление нагнетания, тем больше этот разрыв. И, если верна методика расчета, то по винтовым компрессорам можно получать к.п.д. около 2 единиц, а по поршневым более 10. Почему получается такой «разбег»? Может потому, что сжатие газа происходит в другой энергосистеме? Ведь по логике для всплывающего пузырька замкнутой является система, где его погружают назад тем же путем. Газ же, в данном же случае, мы сжимаем компрессором именно в газовой среде, для которого «замкнутой» должна быть система, при которой он бы расширялся по тем же законам, по которым и сжимался. Но, как видно из практики,, газ сжимается, как правило, изотермически, адиабатически или политропно, а расширяется, всплывая в жидкости – произвольно, т.е. изобарически? И не секрет, что при изобарном расширении газ способен выполнить большую работу, чем затрачивается, при перечисленных выше, способах сжатия. Может и в этом причина. Ведь, если внимательно вглядеться в формулу работы, совершаемой при всплытии пузырька газа в жидкости, то можно заметить, что она аналогична работе расширяющегося газа изобарического процесса. А=pqh(V1+V2)/2 , где pqh=P , т.е. работа газа равна произведению давления на изменение его объема; А=PdV. Это и есть, как мне кажется, еще один признак ,только 2-го рода. Судя по графикам, к.п.д. возрастает при росте давления, т.е. нужно увеличивать общую длину цепи двигателя для получения более высокого прироста энергии. Для этого не обязательно конструировать преобразователи одной длины, можно использовать следующую схему: Дабы не быть заподозренным в плагиате, поясняю, что есть заявка на данную идею.
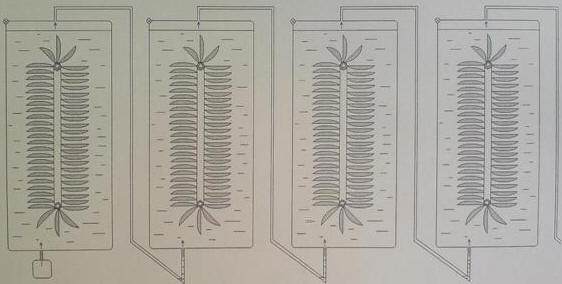
Достоинства такой конструкции очевидны: возможность простого технического изготовления и обслуживания ; возможность изготовления компактных механизмов под любые компрессоры, т.е. любой мощности; отдельные резервуары и, находящиеся в них чаши, позволяют изготавливать их под соответствующее давление расширяющегося газа для каждого резервуара; способность сохранять запасенную мощность сколь угодно долго при остановке двигателя . В рабочее состояние такую конструкцию привести не сложно. Достаточно заполнить все резервуары жидкостью и продуть компрессором. Давление газа в перепускных коленах создаст пневмозатвор, соответствующий давлению каждого резервуара. Излишки жидкости вытекут через последнее колено наружу. Существует мнение, что такая конструкция не сможет работать в режиме «вечного двигателя», поскольку энергия расширяющегося газа берется из жидкой среды и она вскоре «замерзнет». Известно, что тепловая энергия из окружающей среды поглощается при адиабатическом расширении газа. В этом процессе этого явлений не наблюдается, к тому же, если кому-то такое утверждение не нравится, то несложно всю эту конструкцию погрузить в мировой океан и пусть она работает себе за счет температуры того же океана, где, согласно некоторым источникам, можно обеспечить все человечество на 14000 лет энергией понизив температуру оного всего на 1К, заодно и решив проблему глобального потепления на планете. Для тех же, кого не убедили вышеизложенные доводы, хотелось бы привести еще один аргумент в свое оправдание, дабы в оглавлении не отражалась одна лишь интрига. Тем, кто знаком с процессом электролиза известно, что скорость его протекания не зависит от давления раствора в электролитической ванне, а зависит только от силы тока и времени протекания процесса. И, применительно к вышеизложенной схеме, можно на любой глубине разлагать воду на кислород и водород, тем самым обеспечив работой преобразователь и, по желанию, получать их в чистом виде по отработке, либо сжечь их там же, увеличив мощность всей установки. При расходе в среднем 4 Квт/час энергии на получение 2куб.м. водорода и 1 куб.м. кислорода так же несложно рассчитать параметры последнего. Верить всему изложенному или нет – право каждого. И, если у кого есть весомые возражения, или другие соображения, хотелось бы их услышать.
"Парадоксы" закона сохранения.
Конечно, речь пойдет о законе сохранения энергии, незыблемость которого неоднократно пытались поколебать не один десяток людей. Вот и я, как-то, хлебая щи* на кухне, в прочем без большого аппетита, подумал: а чем я хуже тех "камикадзе"? "Пошатаю"- ка я его родименького, а заодно и обосную работу пневмогидравлического преобразователя механической энергии в электрическую. На том и порешил, и построил следующую логическую цепочку рассуждений: Начну я ее, что бы была основа для сравнения, с определения работы силы Архимеда при погружении и всплытии твердого тела. Для этого проделаем умозрительно такой опыт: Пусть в емкость с водой мы погружаем твердое тело в виде куба, имеющего положительную плавучесть. Будем рассматривать только работу архимедовой силы. Работы силы тяжести, зависящую от массы самого тела, пока касаться не будем, поскольку она не играет особой роли, т.к. у рабочей чаши, симметрично ей относительно верхнего шкива, находится чаша холостого хода, которая и компенсирует эту силу. Чтобы описать процесс выполнения работы при погружении и всплытии тела и закон сохранения энергии, рассмотрим детально все силы, задействованные в данном процессе: Погружая твердое тело объемом V на глубину H, мы совершаем работу по преодолению силы Архимеда, которая равна А=pgVH, где pgV-сила Архимеда, а H-путь перемещения тела. Она имеет отрицательное значение, поскольку мы затрачиваем энергию на погружение тела. Соответственно, всплывая, тело под действием той же силы Архимеда совершит ту же, только теперь положительную, работу и закон сохранения энергии будет выглядеть как равенство работ всплытия и погружения тела, разумеется, с разными знаками. Это при погружении и всплытии тела строго вертикально, т.е. тело пройдет тот же путь по той же траектории. Погружая тело, мы создаем потенциал, который определяет две величины, объем вытесненной жидкости и глубина погруженного тела, что наглядно отражено на прилагаемом рисунке.
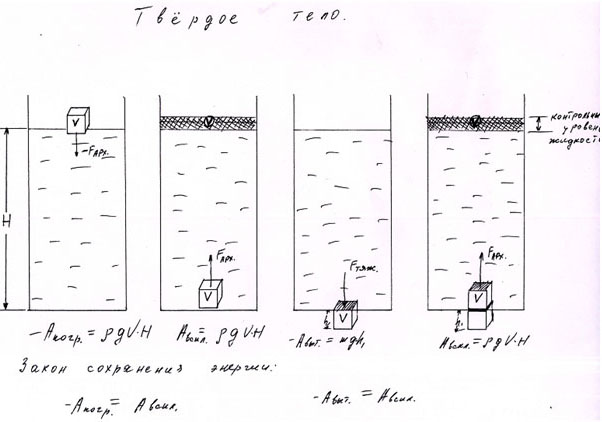
На дне емкости он достигает максимального значения. Если внимательно вглядеться в формулу работы, то ее можно интерпретировать немного по-другому: произведение pgH дает нам гидростатическое давление в точке максимального погружения тела и, поэтому, работа определяется как произведение гидростатического давления на объем погруженного тела. Что это нам дает? А дает нам то, что, если мы поместим, (не погрузим), тело объемом V в точку с данным гидростатическим давлением, то выполним такую же по величине работу, что и при погружении. Хочу сразу уточнить: такую же точно работу, что и при погружении твердого тела, т.е. тела не меняющего свой объем при выполнения этой работы. Это важно, поскольку эта точка может иметь двойной потенциал, что я постараюсь доказать в дальнейшем. Поместить данное тело в точку заданного гидростатического давления технически не сложно, скажем, устроить ему точную по размерам нишу на дне емкости с уровнем верхней грани куба уровню дна этой емкости. Останется только приподнять куб на высоту его ребра и мы с заданием справимся, выполним работу равную pgHV. Теперь, благодаря знаменитому возгласу Архимеда, вспомним, что твердое тело с объемом V вытеснит точно такой же объем жидкости, в нашем случае воды, поэтому в формуле вместо объема твердого тела мы можем поставить точно такой же объем воды, тогда получим, что работа равна гидростатическому давлению воды умноженному на объем вытесненной воды, где pgH=mg/S (m масса воды, давящая на грань куба, S площадь этой грани) и формула примет вид А=mgV/S ( а V=Sh, где h высота куба), подставляя вместо V его значение, получим А=mgSh/S или А=mgh, т.е. работу силы тяжести. Можно было еще проще придти к этой формуле, поменяв сразу pV на m, но тогда было бы не так наглядно и понятно. В итоге получается, что в случае помещения тела в точку заданного гидростатического давления, нужно просто "приподнять" столб жидкости на высоту тела. Подтверждение последнего можно также проследить по рисунку. В обоих случаях куб находится на одинаковой глубине и контрольный уровень жидкости также одинаков. Казалось бы, все и так было очевидно, но давайте не будем торопиться с выводами, продолжим дальше. Чтобы проверить правильность наших рассуждений, зададим в формуле конкретные значения. Пусть куб имеет длину ребра 1метр, тогда его объем- соответственно 1 куб. м., плотность воды 1000 кг/куб.м., g=10м/с2,H=10 м. Работа по погружению, а равно и всплытию тела равна А=1000*10*1*10=100 000 (Дж).Работа по помещению в заданную точку тоже равна А=10 000*10*1= 100 000(Дж). Закон сохранения энергии строго выполняется, т.е. работа перемещения тела по замкнутому контуру в потенциальном поле равна нулю, и нет тут никакой точки двойного потенциала. Да, но это только для случая, когда тело не изменяет свой объем при всплытии или погружении. Мы рассмотрели случай с твердым телом для того, чтобы было с чем сравнивать в дальнейшем, а так же для того, чтобы можно было нарисовать графики работ для обоих вариантов. В данном примере они идентичны. Теперь рассмотрим точно такой же случай, только теперь с телом, меняющим свой объем при погружении и всплытии. Для этого возьмем сильфон (замкнутый сосуд для газов, меняющий свой объем в одном направлении при сжатии или расширении газа внутри него) точно такой по форме и объему, как в предыдущем опыте, с воздухом атмосферного давления и станем его погружать. Работа по погружению тела с переменным объемом, или работа переменной силы, находится как произведение переменной архимедовой силы на глубину погружения сильфона А=pg(V+v)/2*H, где (V+v)/2 среднеарифметическое значение обьема сильфона или, интерпретируя, получим А=pgH(V+v)/2 т.е. произведение гидростатического давления в точке погружения на средний объем сильфона. Соответственно, работа всплытия этого сильфона будет равна по величине, но с противоположным знаком. Закон сохранения энергии не нарушается, с условием, что скорость погружения и всплытия сильфона одинаковы. Если мы зададим теперь сильфону такие же параметры, что и в случае твердого тела, то получим следующую величину работы: А=1 000*10*10*(1 +0,5)/2=75 000(Дж), где v - объем сильфона на глубине 10 метров, согласно закона Бойля-Мариотта.
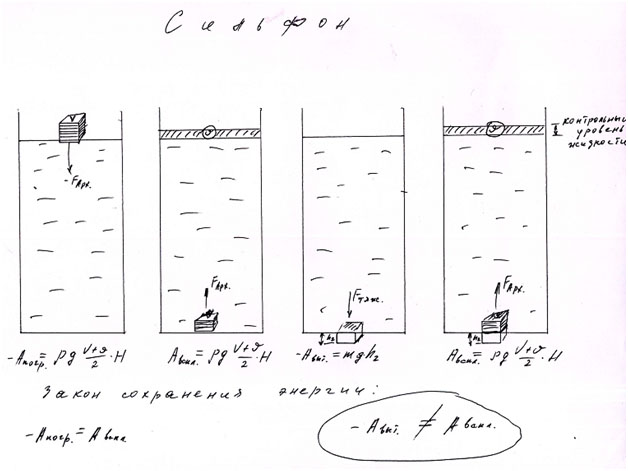
Из этого опыта видно, что, по отношению к твердому телу, работа затрачена меньше на четверть, по причине уменьшения объема сильфона при погружении, и это видно по контрольному уровню жидкости, если сравнить изменение этого объема с уровнем в случае твердого тела. Теперь попробуем поместить сильфон в точку заданного гидростатического давления, как в первом опыте, чтобы так же выполнялся закон сохраненияэнергии. Мы этого сделать не сможем, поскольку нам нужен среднеарифметический (не минимальный) объем сильфона, а такое условие невыполнимо. Хотя, казалось бы, почему мы не можем взять сильфон такого же минимального объема, что и в нижней точке емкости и поместить его в точку заданного гидростатического давления. Давайте разберемся, почему?: Дело в том, что сильфон, с изначальным атмосферным давлением внутри него, надо сжать до давления, равного гидростатическому, и лишь потом мы сможем " приподнять" столб воды, т.е. нужно выполнить работу по сжатию воздуха в сильфоне и работу против силы тяжести столба воды. А теперь давайте подсчитаем, во что это нам "обойдется".Чтобы было понятнее, расчеты будем производить по конкретным значениям. Сильфон с воздухом до нужного объема т.е. 0,5 куб.м. мы можем сжать любыми существующими способами, но мы, для простоты эксперимента, просто придавим его телом массы 10 000 кг., или слоем воды высотой 10 метров т.е. А=mgh=10 000*10*0,5=50 000(Дж). Чтобы "приподнять" столб воды, потребуется еще столько же: А=mgh=10 000*10*0,5=50 000(Дж), итого -100 000Дж, как для случая твердого тела. Но мы-то знаем, что при всплытии сильфон сможет " выдать" только 75 000Дж .Так же и с любым другим объемом, закон сохранения энергии не выполнится. Даже если мы поместим туда среднеарифметический объем сильфона, согласно формуле, то получим еще больший разрыв в результатах. В любом случае, мы не сможем в нижней точке, названной точкой двойного потенциала, подобрать объем сильфона, согласно его параметров в верхней и нижней точках, чтобы закон сохранения энергии выполнился, как в случае твердого тела. В этом и сокрыт момент истины, и это нужно принять как аксиому. Хорошо это или плохо? Для закона сохранения энергии может и плохо, поскольку это меняет у нас представление о нем как о законе, для нас же это наоборот - благо, поскольку позволяет получать нам, так называемую", свободную" энергию. Для этого нужно, после сжатия в сильфоне воздуха, открыть клапан, чтобы он "потеснил" воду, используя энергию затраченную на сжатие этого сильфона, а ее у него вполне достаточно. И тогда получается, что мы затрачиваем энергию только на сжатие воздуха, которая равна, как мы выяснили, работе силы тяжести А=mgh.
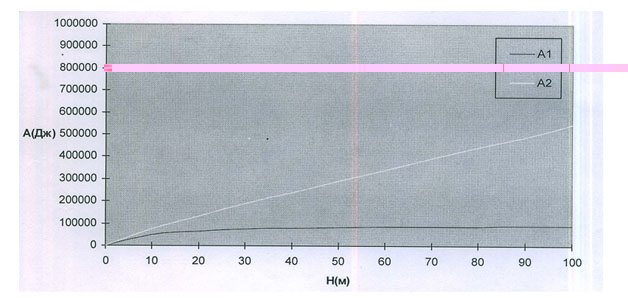
Наглядно эта разница затраченной и полученной работ видна на прилагаемом графике. Мне могут возразить, что, как только мы откроем клапан сильфона, давление в нем упадет, и воздух не сможет в дальнейшем поступать в жидкость. Конечно, может быть и такое, но только в случае единичного акта, но при постоянном "поддавливании" компрессором воздуха, как при работе преобразователя, этого не случится. Хотелось бы сразу сделать оговорку, мы производили расчеты приблизительно, для идеального случая, поэтому таких же результатов в реальной жизни мы не добьемся, но это не нивелирует результат. Доказательством этого могут быть расчеты, произведенные по конкретной модели компрессора и ссылка на графики удельного расхода энергии, согласно справочника Рахмилевича З.З. "Компрессорные установки". Далее возникает резонный вопрос: Почему все-таки с твердым телом выполняется закон сохранения энергии при введении его в точку заданного гидростатического давления, а для тела меняющего объем при всплытии или погружении, то бишь газа - нет?. Может интерпретированную формулу нельзя применять для газа? А почему же "нет", мы же в состоянии нагнетать газ, так же как и помещать твердое тело, на любую глубину жидкости т.е. в любую точку заданного гидростатического давления?. Ответ, очевидно, однозначен: Это две разные энергетические системы. Внутренняя энергия твердого тела инертна при всех перемещениях его в жидкости, что обусловлено свойствами твердого тела, а внутренняя энергия газа, как в сильфоне, так и самого по себе, активна по отношению к внутренней энергии жидкости, в которой он находится, что отражается в изменении объема всплывающего или погружающегося тела с газом. Взаимодействие внутренних энергий жидкости и газа - дает в итоге результаты, полученные в опыте, только теперь, в совокупности, он не подчиняется известному нам закону. По отдельности,- погружение и всплытие сильфона- это одна энергосистема, а сжатие и расширение газа в сильфоне или вне его - это другая. В качестве подтверждения хотелось бы привести еще парочку примеров "казуса" закона сохранения энергии: Опыт старый, только с некоторыми изменениями. Тот же сильфон мы погружаем на 10 метров, затратив, как известно, 75 000Дж. В нижней точке мы "переводим" его в "твердое" тело, проще говоря, фиксируем по высоте, чтобы предотвратить его расширение. Всплывая он, имея объем 0,5куб.м., выполнит работу 50 000Дж. Остальные 25 000Дж, по логике, должны остаться в сжатом воздухе сильфона. Но мы-то знаем, что в сжатом сильфоне от объема 1-го куб.м. до объема 0,5куб.м. находится 50 000Дж. Откуда взялось еще 25 000Дж в сильфоне? Собственно, они там и были в нижней точке погружения, там же и остались, но, тем не менее, закон сохранения энергии не выполнился. А теперь сделаем наоборот: Сжатый сильфон, с известными нам 50 000Джоулями, погрузим в нижнюю точку, затратив еще 50 000Дж, там разфиксируем и позволим всплыть. Получается, затратили 100 000Дж, а получили - 75 000Дж. Куда делись 25 000Дж - непонятно. Конечно, можно предположить, что вторгаясь в естественный процесс, мы "ломаем" его законы, но ведь это нам на руку. Хотя хотелось бы заметить, что в законах физики наши познания распространяются до определенной грани, за границей которой, мы не можем объяснить, почему так происходит, а принимаем все как данность. И до сей поры это никого не смущает. Однако если возникает где - то прецедент получения, так называемой, свободной энергии, то это вызывает искреннее возмущение некоторых умов, а вот "рассеивание" ее в окружающем пространстве без пользы - процесс нормальный? По сути же, мы находимся внутри энергетической системы и любое пользование энергией этой системы общий баланс не изменит, а лишь приводит к преобразованиям энергии внутри нее, что в доказательстве, как мне кажется, не нуждается. Это так, в виде отступления. А теперь вернемся к нашим " баранам". Так вот, в "никмике" для получения энергии и используется случай, когда энергия "возникает". Сжимается воздух вне жидкости, а получаем при его расширении по мере всплытия. Тут может опять возникнуть вопрос: Может погружение газа в жидкую среду - это тоже способ его сжатия, кроме нам известных изотермического, изобарического, изохорического, политропного или, тем паче, произвольного? Хотя произвольное сжатие газа как-то не возникает в воображении, известно произвольное расширение газа, вероятно это и есть случай всплывания газа в жидкости. Но тогда это произвольное расширение обуславливается еще и законами среды, окружающими газ. Хотелось бы верить, но если бы в нашем случае было произвольное всплытие сильфона, то не было бы "провалов" в законе сохранения энергии. А так выходит, что внутренние энергии газа и жидкости - это две разные энергосистемы т.е. мы имеем дело в целом с разомкнутой системой, потому и не выполняется этот закон. Подтвердить это, повторюсь еще раз, может и такой факт, как явление электролиза той же воды. Ведь по закону Фарадея объем вещества, выделившегося на электроде зависит от количества электричества, прошедшего через электролит, а не от давления в электролитической ванне. И как в этом случае должен вести себя закон сохранения энергии, он ведь не "знает", на какой глубине мы собираемся разлагать воду и применять газы ее составляющие для работы? Отсюда, исходя из вышесказанного, напрашивается следующий постулат: " Любой физический или химический процесс, происходящий в жидкости и идущий с образованием газа, может иметь положительный баланс энергии, полученной при всплытии, по причине разомкнутости энергетической системы". Потому-то я и назвал нижнюю точку погружения точкой "двойного потенциала", поскольку из этой точки газ может расширяться двумя путями:- назад, по пути его нагнетания - меньшего потенциала, либо всплывая - по пути большего потенциала. А цикличность процесса позволяет создавать механизмы для получения энергии, и ее потребления, без затрат топлива, а лишь за счет разных свойств жидкости и газа в поле гравитации, обуславливающий этот процесс. Конечно, закон сохранения энергии я может и не «пошатнул» основательно, но догме, запрещающий получение халявной работы, я, надеюсь, репутацию подпортил.
Щи, к тому времени, как мне показалось, приобрели другой вкус, и стали вполне съедобны.
Хлебать щи* - осмысливать законы природы (жаргон.)
Николай Миколюк. г. Тында, Амурская обл.